예전에 회사에서 일할 때, 초당 30만건 정도 들어오는 자료의 빈도를 세서 누적 데이터를 기준으로 5분, 1시간, 1일, 1주, 1달, 1년 최다 순서로 100개 정도씩을 보여주는 루틴을 만들 일이 있었습니다. 그 때는 뭐 회사 프로젝트도 검수 기간도 다 끝나고 영 제값 못 받고 한다고 생각하는 프로젝트였기 때문에, 그냥 대충 가장 단순하게 막 구현을 했더니 오방 느려서 하드웨어빨로 버티고 있었습니다. 나중에는 각 샘플링 별로 상위 10배수를 뽑아서 나머지를 버리는 등의 튜닝을 약간 해서, 처리속도가 데이터 들어오는 것을 못 따라가는 문제를 약간 해결해야하긴 했습니다. 🙂
물론 이렇게 하면, 정확한 이산 데이터를 합해서 하기 때문에 아주 정확한 자료를 얻을 수 있다는 장점은 있지만, 통계 기간에 들어가는 샘플의 수가 워낙 많기 때문에 속도의 문제나 기간의 제한 등 여러가지 문제가 산적해 있었습니다. 특히 가장 문제는, 샘플 저장 수를 줄이기 위해서 장기간의 통계용 샘플들은 정밀도를 줄여서 5분 데이터를 모두 모아서 1시간 데이터로 만드는 등의 작업을 거치기 때문에, 업데이트가 바로바로 되지 않는 문제가 있었습니다. 그래서, 그때는 그냥 뭐 병특도 끝나가고 해서 대충 넘어 갔는데 -ㅇ-, 얼마전에 여자친구 숙제를 도와주다가, 커널에서 load average 계산하는 방법을 보고서 이것을 게시판의 “최근 뜨거운 글 100개 목록”이나, 네트워크 장비들의 “최근 다발 접속 IP 100개” 같은 통계에 쓰면 좋겠다는 생각이 들었습니다. +_+ 벌써 다른 데서는 다 쓰고 있었는지도 모르겠지만; 이렇게 되면 보통 하듯이 하루 단위로 리셋되지 않고 부드럽게 꾸준히 업데이트되기 때문에 비교적 부하를 줄이면서도 쓸만한 데이터를 얻을 수 있지 않을까 싶네요~
그래서, 그 방법이 무엇이냐!
간단히 요약해서 다음 수식으로~
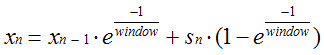
커널 소스코드에서는 sys/kern/kern_synch.c 부분에 있습니다.
x가 로드이고, s가 새로 들어오는 샘플, window가 원하는 통계 기간의 샘플 수 입니다. 이렇게 하게 되면, 새로 들어오는 샘플은 1-1/exp(1/window) 의 비율로 들어가고 그 다음부터는 1/exp(1/window)가 계속 곱해져서 살짜쿵씩 사그라듭니다. 적당히 원하는 보존 기간을 지나가면 무시할 수 있을 만큼의 비율로 없어지기 때문에, 데이터 값 1개만 유지하고서도 이산형 데이터 모두를 저장하는 부담을 줄일 수 있다는 점에서 그런대로 쓸만한 방법인 것 같네요. +_+
그래서, 과연 이 놈이 진짜로는 어떻게 없어지나 그래프를 한 번 그려 봤습니다. (x 축이 축적 횟수, y축이 최종 데이터의 반영 비율, 샘플 누적 목표는 10으로 했을 때)
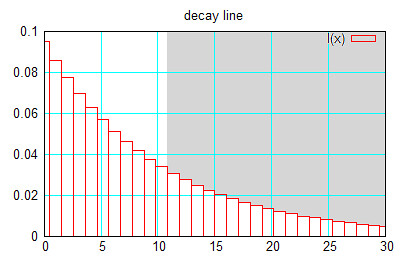
그래서 대략 계산해 보면, 10개까지의 데이터들의 반영 비율이 63% 정도 되고, 2배수인 20개까지의 비율의 합이 86%정도 됩니다.
정확한 데이터는 아니지만, 데이터 계산을 연속적으로 할 수 있고 연산/저장량이 많이 줄어든다는 점이 장점이겠습니다.
그런데, 커널에서는 부동소수점 연산을 피하기 때문에, 이런 계산을 좀 더 재미있는 방법으로 하고 있는데, 이것도 한 번 눈여겨 볼 만합니다. 🙂 커널 소스의 cexp라는 fixpt_t형 배열에는 exp(-1/샘플수)의 값이 미리 계산이 되어 있어서 그냥 곱하기만 하면 되게 되어있기 때문에 e 계산이나 나누기를 하지 않아도 됩니다. 그리고, 사실은 이놈이 부동소수점형이 아니라, CPU에서는 정수형으로 취급되는 고정소수점형이라는 것~ 32비트 중에서 왼쪽 21비트를 정수영역, 나머지 11비트를 소수점영역으로 쓰는데, 1<<11 * 소수 이렇게 하면 간단하게 소수점 이하라도 쉽게 변환이 되고, 덧셈 뺄셈도 생각해 보면 그냥 정수 덧셈,나눗셈 인스트럭션으로 될 것을 알 수 있습니다. 그리고, 곱셈도 가능한데 둘을 곱한 다음에 소수 영역 길이인 11비트만 오른쪽으로 시프트 해주면 고정소수점 곱하기 한 것처럼 됩니다. (물론, 손으로 써보면 쉽게 증명이 됩니다. 🙂 후배한테 자랑했더니 요새는 학교에서 이런 것도 가르쳐 준다는군요 -.-;)
뭐 하여간.. 전에 회사에서 바쁘던 와중에 검색을 할 때는 좋은 아이디어가 딱히 안 떠오르고, 검색을 해 봐도 딱히 좋은 알고리즘이 안 떠올랐는데, 계속 곱하기만 해도 줄어든다는 것을 떠올리지 못한 것은.. 아무래도 수학 공부를 안 해서일까요 -.-a 그래서 이번 학기에 공수 불끈! +_+
공수는 수학이 아니에요( 라고 주장하고 있습니다. ㅜㅜ )
공수에서 수학적인 아름다움이나 감동을 느끼긴 힘들더라고요. ㅜㅜ
저는 음함수미분을 요리 해도 되고, 조리 해도 되고, 뒤집어도 되고 해서 우와 신기하다 하면서 놀고 있어요 ㅋㅋㅋㅋ
아하ㅡ 어제 그린다던 그래프가 요거였구나~ ^^
아하~ 어제 gnuplot 으로 그리신다던 그래프가 요거였군요~^^
이 글에서 주의깊게 보아 할 것은 “여자친구 숙제를 도와주다가” !!!
숨은 염장에 주의 ㅎㅎㅎㅎ
부러워용 🙂 제숙제도 해주시면 이산구조 숙제 보너스…..가 아니지 -_- 흑;
제 여자친구는 학교 다닐때 두께가 n이고 지름이 m인 강철관에 시간당 x만큼의 물이 지나갈때 강철관이 받는 압력은 얼마인가…. 라던가 하는 문제를 풀고 있길래,
“적당히 받는다.. 라고 써..” 라고 했던 기억이 나서 부끄러워지는군요… ;ㅁ;
으으으.. 공식이랑 그래프봐도 잘 모르겠어요
대~충 어떤 원리라는거 정도 감 잡는중
제 여자친구는 이런 어려운 숙제 안해서 다행.. =3=3
킁킁. 숨은 염장 숨겨뒀는데 발견하셨 =3=3
이런.. 스윽.. 하고 읽을 수 밖에 없는 글을!
쓰셨군요. 🙂
여자친구가 없어서 다행! =3
이거는 샘플의 평균을 낼 수는 있지만 샘플중 최빈수 순서대로 n개를 바로 추려내는데 쓸 수 있는 공식은 아니지 않나요? 잘 이해가 안 갑니다만.
최빈수 n개를 추려내는 용도로 바로 쓰는 것은 아니고용, 최빈수 n개를 구하기 위한 각 개체의 빈도를 누적하기 위한 용도로 쓸 수 있습니다. 정렬 알고리즘의 복잡도를 무시하면 전체적인 알고리즘의 복잡도가 O(N²)에서 O(N)으로 줄어들겠지요~
최빈수 n개를 구하기 위한 각 개체의 빈도를 누적하기 위한 용도!
소주랑 신경안정제랬던가…어디뒀었지?(뒤적뒤적…)
초당 30만건이라…. 뭘까요? -,-;;; 긁적긁적..
머신이 아무리 좋다해도 초당 1000건은 안 넘을텐데…
1000대쯤으로 서비스하는 것인가요? 으음.. 암튼 많군요..
대충 쿼리를 기준으로 이진트리를 만들어, 이진검색을 한뒤 기록하는 방식으로
5분단위로 잘라서 하면, 한번에 9000만건을 처리해야되는데..
1건당 0.00001초 걸린다고 하면 대략 난감하군요…
이런 경우는 대략 표본추출해서 (9000만건중 100만건) 통계내야될것 같은데..
전수조사는 뭔가 불가능한듯한… -,-;;;
전수조사를 할 때 지역 통계 노드에서 직접 조사를 해서 간추려서 상위 노드로 보내 주면 됩니다. 🙂
음…그렇다면 매번 인스턴스가 도착할때마다 누적계산을 해줘야 하니 최빈수 n개를 구하는 데에는 쓸 수는 없을 것 같군요. 예를들어 접근하는 ip주소 만개에서 백만번 액세스 할때 가장 자주 나타나는 ip주소 100개를 뽑자면 만개의 데이터값 공간을 매번 주소가 들어올때마다 계산해줘야 한다는거니까요. 100개의 데이터값 공간만 가지고 하기는 곤란한듯 합니다.
그리고 위에 궁금하신분께는 초당 30만건이란건 전국단위의 전화호출건수나 문자메시지같은 걸 처리하는 시스템일겁니다. 그런건 보통 컴퓨터 한대로 처리하게끔 만들수도 없고 그렇게 만들지도 않죠. (최고성능의 cpu도 초당 인터럽트 십만개정도가 한계니까…다른거 못하고 인터럽트만:)
앙, 별 상관없는 부분에 말꼬리같아 쫌 그렇지만, 이부분,
“최고성능의 cpu도 인터럽트 십만개정도가 한계”라는 말씀에 대해서 주제넘게 말씀드리자면, 그건 os scheduler의 설계에 따른거지 절대 100k/s가 한계가 아닙니다.
아마도 tick을 염두에 두고 하신 말씀같은데, 실제론 cpu의 instruction cycle과 isr의 opcode양에 따라 다르게 되죠.
당근 scheduler의 설계에 따라서도겠으나, 순전히 hardware에 입각해서 보자면 interrupt 속도는 int assert, isr vector jump, isr itself.의 clock cycle수만큼 빠릅니다.
머 3GHz clock cycle machine에 local interrupt라고 하면, 열번 접고 저거 대충 100 clock잡아먹는다고 쳐도 30MHz의 속도로 interrupt를 처리할수 있다는 결론이 나오게되죠. 즉 30M/s가 됩니다.
앙, 역시 넘 썰렁행..ㅠ.ㅠ;
물론 그런 걸 100개 가지고 전체를 조사하는 방법은 있을 수가 없습니다.
제가 언급했던 사례에서는 약 80MB마다 꾸준히 rotate되면서 계속 append가 되는 텍스트파일을 보고 있는 데몬이 있어서, 그 데몬이 자료를 간추려서 상위 노드로 보내 주게 되어 있는데, 기존에는 해시테이블로 1분마다 reset 하면서 카운트를 했습니다. 이걸 exponential decay를 쓰면 reset 없이 깔끔하게 자료를 만들 수가 있구요. 그리고, 단순 조사를 하는 경우 1분 샘플을 올려서 5분이나 1주 샘플을 만들 때에 5분치나 1주치를 queue에 쌓고 있어야하는데, 이런 부담이 확 줄어들게 되는 장점이 있습니다.
그러니까, 쌓고 있는 데이터가 {개체수}*{샘플추적기간} 이 아니라 {개체수} 의 데이터만 쌓아도 된다는 장점이 이 글에서 말한 원래 목적입니다. 샘플추적기간이 길어지면 이 방법을 도입하는 것 만으로도 100배 이상으로 줄일 수가 있습니다. 그 외에도 최소 누적기간이 1분이라 하더라도, 샘플이 1초마다 들어오면 1초마다 모든 데이터가 다 업데이트될 수 있기 때문에 반응성이 뛰어난 최빈수 목록을 만들 수가 있습니다~
그래서, 제목이 “최빈수 n개를 뽑기”가 아니라 “최근 얼마 간의 데이터 쌓기” 이죠. 🙂
“전수조사를 할 때 지역 통계 노드에서 직접 조사를 해서 간추려서 상위 노드로 보내 주면 됩니다.”
으음.. 그런 간단한 방법이 -,-;;;;
제가 읽기론 들어오는 쿼리를 해쉬테이블로 구성한 후에 로드를 기록한다는 것 같은데… 로드 대신에 그냥 카운트를 해도 되지 않나요?
결국 기존로드와 새로 들어오는 샘플간에 가중평균을 하는셈인데..
커널에 expotential함수의 값이 테이블로 존재한다고 하더라도, 역시 컴퓨터가 좋아하는 정수형으로 기록하는 것이 가장 확실하고 또한 간단하지 않을까요?
x_n 1 = r* x_n (1-r) * s 보다
x = x 1 하는게 낫지 않나요?
음 더하기 표시가 안되는군요..
x_n 1 음 x_n plus 1
x = x 1은 x=x plus 1
그냥 덧셈을 하면 1분간의 자료를 쌓는다면, 1분마다 0으로 리셋을 해 주던가, 1분이라는 기간을 생짜로 자료를 넣어 둘 수 있는 큐나 리스트 같은 것을 유지해야겠죠~ exponential 하게 줄어든다는 것은, 앞에서도 계속 언급했지만, 연속적인 자료를 얻을 수 있다는 것이 가장 장점입니다. 테이블도 필요 없어요~
아..
통계시간별로 window크기를 조정해서 처리한단 말씀이군요..
(흐흐.. 계속 이해 못하고 있었음..)
저도 비슷한 걸 짜본적이 있는데..
딱 위의 6줄에 해당하는 방법으로 ㅋㅋㅋ
http://cs.nyu.edu/cs/faculty/shasha/papers/statstream.html
대전 K대에 오시면 식사라도 한번.
퍼키님 팬이라서 ㅡㅡ;
오.. 그런 것에 대한 논문도 있었군요.. 감사감사 +_+
크.. 대전에 가면 번개를 자주 하려고용~ ^.^;;